Bernoulli's Principle(Incompressible flow equation)

In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy.The principle is named after Daniel Bernoulli who published it in his book Hydrodynamica in 1738.

Bernoulli's principle can be applied to various types of fluid flow, resulting in what is loosely denoted as Bernoulli's equation. In fact, there are different forms of the Bernoulli equation for different types of flow. The simple form of Bernoulli's principle is valid forincompressible flows (e.g. most liquid flows) and also for compressible flows (e.g. gases) moving at low Mach numbers (usually less than 0.3). More advanced forms may in some cases be applied to compressible flows at higher Mach numbers (see the derivations of the Bernoulli equation).

Bernoulli's principle can be derived from the principle of conservation of mechanical energy. This states that, in a steady flow, the sum of all forms of mechanical energy in a fluid along a streamline is the same at all points on that streamline. This requires that the sum of kinetic energy and potential energy remain constant. Thus an increase in the speed of the fluid occurs proportionately with an increase in both itsdynamic pressure and kinetic energy, and a decrease in its static pressure and potential energy. If the fluid is flowing out of a reservoir, the sum of all forms of energy is the same on all streamlines because in a reservoir the energy per unit volume (the sum of pressure andgravitational potential ρ g h) is the same everywhere.

Bernoulli's principle can also be derived directly from Newton's 2nd law. If a small volume of fluid is flowing horizontally from a region of high pressure to a region of low pressure, then there is more pressure behind than in front. This gives a net force on the volume, accelerating it along the streamline.

Fluid particles are subject only to pressure and their own weight. If a fluid is flowing horizontally and along a section of a streamline, where the speed increases it can only be because the fluid on that section has moved from a region of higher pressure to a region of lower pressure; and if its speed decreases, it can only be because it has moved from a region of lower pressure to a region of higher pressure. Consequently, within a fluid flowing horizontally, the highest speed occurs where the pressure is lowest, and the lowest speed occurs where the pressure is highest.

Incompressible flow equation

In most flows of liquids, and of gases at low Mach number, the density of a fluid parcel can be considered to be constant, regardless of pressure variations in the flow. Therefore, the fluid can be considered to be incompressible and these flows are called incompressible flow. Bernoulli performed his experiments on liquids, so his equation in its original form is valid only for incompressible flow. A common form of Bernoulli's equation, valid at any arbitrary point along a streamline, is:

(A)

where:

 is the fluid flow speed at a point on a streamline,

 is the acceleration due to gravity,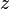

 is the elevation of the point above a reference plane, with the positive z-direction pointing upward – so in the direction opposite to the gravitational acceleration,

 is the pressure at the chosen point, and

 is the density of the fluid at all points in the fluid.

For conservative force fields, Bernoulli's equation can be generalized as:

where Ψ is the force potential at the point considered on the streamline. E.g. for the Earth's gravity Ψ = gz.

The following two assumptions must be met for this Bernoulli equation to apply:

• the flow must be incompressible – even though pressure varies, the density must remain constant along a streamline;
• friction by viscous forces has to be negligible. In long lines mechanical energy dissipation as heat will occur. This loss can be estimated e.g. using Darcy–Weisbach equation.

By multiplying with the fluid density , equation (A) can be rewritten as:

or:

where:

 is dynamic pressure,

 is the piezometric head or hydraulic head (the sum of the elevation z and the pressure head) and

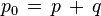 is the total pressure (the sum of the static pressure p and dynamic pressure q).

The constant in the Bernoulli equation can be normalised. A common approach is in terms of total head or energy head H:

The above equations suggest there is a flow speed at which pressure is zero, and at even higher speeds the pressure is negative. Most often, gases and liquids are not capable of negative absolute pressure, or even zero pressure, so clearly Bernoulli's equation ceases to be valid before zero pressure is reached. In liquids – when the pressure becomes too low – cavitation occurs. The above equations use a linear relationship between flow speed squared and pressure. At higher flow speeds in gases, or for sound waves in liquid, the changes in mass density become significant so that the assumption of constant density is invalid.